Deep Learning in Brain Imaging

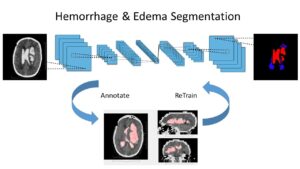
In this article we discuss several recent leading works about Deep Learning in brain imaging and brain microscopy. We organize the works in subsections according to the general algorithmic tasks: segmentation, registration, classification, image enhancement or other tasks. The categories are not always mutually exclusive, and the works address different medical tasks and modalities, as we describe next in more detail.

2.1 White matter imaging

One of the challenging tasks in MRI data analysis is the tracking and clustering of white matter fibers. Fibers are typically densely packed, with crossing fibers, and a wide range of geometries, which make the reconstruction of streamlines from raw diffusion signals (dMRI) a hard task. The success in this task is measured according to connection identification accuracy and recall, as well as according to the related volumetric overlap and overreach of the prediction with the ground truth. These two metrics are often summarized in the F₁ score.

Recent advancements involve different uses of deep learning, from direct use of CNNs and recurrent networks to novel architectures and hybrid algorithms. [50] use Multi-Layered Perceptrons (MLPs) and Gated Recurrent Unit (GRU) neural networks to learn fiber tractography directly from weighted diffusion signal. They find that exploiting past information within a streamline trajectory as additional input during tracking helps to predict the following direction, and that recurrent networks have a significant advantage over MLPs for this task. The models are evaluated on data from the ISMRM 2015 tractography challenge and achieve 64.4% true positives, 35.5% false positives and F₁ = 64.5% – reaching above 15% improvement in F₁ score over previous results.

Other approaches include non-direct use of deep learning. [71] suggest a two-step algorithm: first they perform a coarse estimation of fiber orientations with a small basis set (i.e., with a coarse angular resolution). For this they use an unfolded and truncated iterative feed forward network (with shared weights between its layers). The second step uses a classic regression approach and solves a regularized least squares problem on a larger basis set (i.e., a finer angular resolution), where the coarse results of the first network are used as l₁ regularization (see Eq 6, 7 in the paper). This ensures that the new learned result is biased towards the previously learned coarse estimate. They obtain qualitatively good results, albeit the evaluation is only on simulated data, and a single real datum from Kirby21. [27] use CNNs to learn shape features of fiber bundles, which are then exploited to cluster white matter fibers – thus avoiding the explicit fiber tracking task, and [70] use deep learning to learn the parameters of an ensemble average propagator (see [33]) for the fiber orientations, instead of learning the orientation directly.

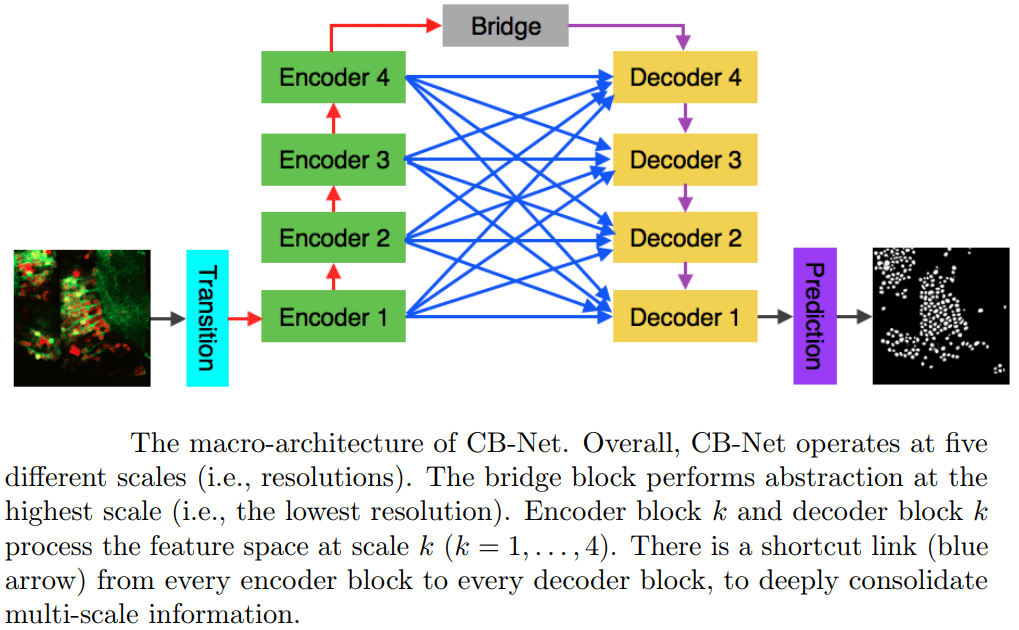
A novel CNN architecture for white matter segmentation is suggested in [14] for optic microscopy images. Their network is composed of nine 3D CNNs in a complete bipartite macro-architecture (see figure below, adapted from their paper). The method was demonstrated for neuronal cells in dual-color confocal microscopy images of zebrafish and not on medical data, but the results and architecture seem promising and highly relevant for other segmentation tasks.

2.2 Segmentation tasks

Many brain imaging tasks involve image segmentation as a direct objective, or as a part of detection, classification or other tasks.

One family of medical tasks that require accurate segmentation is tumor and lesion detection and characterization. Fully Convolutional Networks (FCN) with an encoder-decoder structure have proven very effective for these tasks, and recent advancements involve modifications and variations of these architectures. [57] use a two-branch FCN architecture for brain tumor segmentation. They improve over standard FCN and FCN+CRF (Conditional Random Field [41]) networks by incorporating boundary information into the loss function. This is done by training one network branch on tumor tissue classification, and the other on tumor boundary classification. The two outputs are concatenated and fused in a 2-layer CNN. They evaluate the model on the BRATS13 and BRATS15 datasets and obtain Dice score of 88% on whole tumor segmentation (1% improvement above FCN and FCN+CRF results) and a finer boundary detection, but with similar detection accuracy to other models.

[22] suggest another CNN architecture to deal with brain tumor segmentation on multimodal data. Their approach is based on splitting a given CNN into two networks – effectively performing a factorization of the feature space into cross-modality features, which are processed in one part of the network, and modality-conditioned features, that are processed in the other part of the network. They achieve similar Dice performance on the same datasets mentioned above. [13] use a 3D CNN with a combination of skip-connections and auxiliary supervision on internal layers for segmentation of intracranial arterial calcification. In training dropout regularization is used in network locations that can be skipped by the skip-connections. They train and validate their network on 882 CT scans and test on 1,000, and achieve a Dice score of 76.2% and report 97.7% correlation between their predictions and manual annotations.

Other recent works using deep learning in brain imaging address the practical hardness of obtaining annotated data for segmentation. [20] show how to train a 3D CNN with “weak labels” that include only the number of lesions per image. In testing, the network predicts the number of lesions with a global pooling layer, and then a mask is produced by removing this layer. They evaluate the method for detection of enlarged perivascular spaces in the basal ganglia in MRI, for assisting early detection of emerging cerebral small vessel disease. Their dataset includes 1,642 3D PD-weighted 1.5T MRI scans and they achieve a true positive rate of 41%, false positive rate of 2% and detection rate of 60%.

Small amounts of labeled data can be dealt with also by training deep learning models on additional data from other modalities. [25] address two practical questions for domain adaptation in medical imaging: “ (1) How much data from the new domain is required for a decent adaptation of the original network?; and, (2) What portion of the pre-trained model parameters should be retrained given a certain number of the new domain training samples? ”. They compare between domain-adapted CNNs and specialized CNNs (trained only on the target domain) on the task of white matter hyperintensity segmentation and find that their domain-adapted networks can achieve similar performance to specialized networks.

Another solution is suggested in [11], who consider a semi-supervised learning approach for training CNNs on Multiple Sclerosis lesion segmentation. The method is based on a U-net-like architecture, and they develop a random feature embedding scheme with an additional loss function to enhance training. The evaluation is on the MSSEG and MSKRI datasets (containing T1, T1.5, T2, T3 and FLAIR MRI). They show that adding semi-supervised random embedding improves the domain adaptation ability. The results are still inferior in terms of F₁ score to specialized training (17-34% vs 37-71%), but the method may be useful when there is too little data of the specific target domain, or as a pre-training tool.

2.3 Volumetric data registration

Registration tasks of volumetric data (e.g., slices to volume, or volume to projection conversions in CT and MRI data) are computationally demanding tasks, and a complete deep learning solution for high resolution 3D registration has not been achieved yet. Two recent works that advance in this direction with brain imaging data are [62] and [29]. Other deep learning algorithms related to registration tasks in cardiology and pulmonology are referred to in the following sections.

[62] address the problem of training CNNs on registration from few training data by using model based data augmentation. They train a FlowNet [19] CNN with this augmented data and show on two small data sets of brain MRI and cardiac MRI with less than 40 training images, that CNNs trained with data augmentation from their generative model outperform those trained with random deformation augmentation, or with displacement fields estimated via classic image registration.

[29] use a CNN to learn a mapping of 2D image slices into their correct position and orientation in 3D space. They evaluate their method on simulated MRI brain data with random motion and on data of fetal MRI and obtain an average prediction error of 7 mm on simulated data, and convincing reconstruction quality of images of very young fetuses. Their experiments show a positive proof-of-concept, and the method may also be applicable to registration of CT and X-Ray projections. The prediction times per slice are a few milliseconds, making it suitable for real-time scenarios.

2.4 Image enhancement

High resolution imaging is especially important in brain imaging due to the densely-packed cell and axon structures. Improved resolution can be obtained by using MRI devices with stronger and more uniform magnetic fields, and by means of improved processing of the MR signal. High magnetic field MRI devices are effective, but expensive and in many hospitals they are not available, and thus improved signal processing methods are an attractive challenge.

Two recent works apply novel deep learning solutions for super resolution in brain MRI scans. [61] use a CNN with variational dropout (see [37]) to create super resolution images from dMRI brain scans, and to estimate the parameter uncertainty of the model for the super-resolved output. They demonstrate through experiments on both healthy and pathological brains from the Human Connectome Project (HCP) and Lifespan datasets the potential utility of such an uncertainty measure in the risk assessment when using the super-resolved images. Their baseline model achieves 8.5%/39.8% reduction in RMSE on interior/exterior regions in respect to state-of-the-art random-forest based method [60].

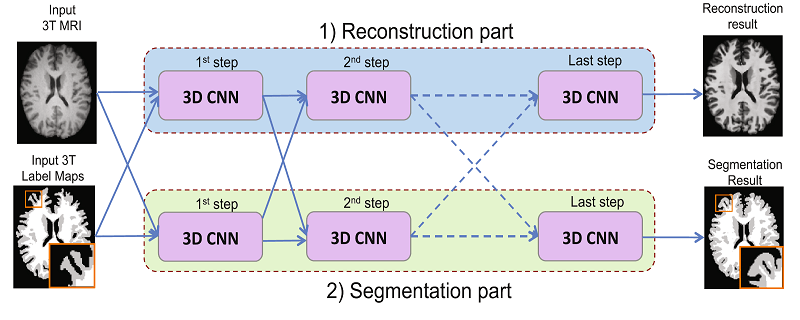
[9] suggest a network architecture that can jointly perform brain tissue segmentation from MRI and super resolution in two parallel parts of a cascaded CNN. The network has two streams, each is a chain of 3D CNNs (see image below). One stream of the network emulates 7T-MRI images from 3T-MRI images (increasing resolution and contrast), and the second CNN stream performs segmentation. This new method shows convincing SR results, and lower Dice scores than competing methods for segmentation, on a dataset of 15 pairs of 3T and 7T MR images collected from 15 healthy volunteers.

2.5 Classification and diagnosis

Two recent works address two of the central challenges in brain disease diagnosis: autism, and Alzheimer’s disease. [39] use Siamese Graph Convolutional Networks to estimate a graph similarity metric between graphs that represent functional connections between brain regions. They run experiments on the ABIDE dataset and show that their method can learn a graph similarity metric tailored for a clinical application, and improve the performance of a simple k-nearest-neighbors classifier by 11.9% compared to the performance of the same classifier with a traditional distance metric (euclidean distance after PCA), for the task of classifying fMRI of patients with autism spectrum disorder, and a control group.

[44] perform simultaneous classification and regression for Alzheimer’s disease (AD) diagnosis, by combining MRI data and personal information of subjects (age, gender, and education level). Specific MRI patches related to AD are selected according to previously suggested data-driven algorithms, and a L-branch CNN is trained on joint disease classification, and on clinical score regression. Each of the L network branches inputs a different brain patch, together with the personal data, and the outputs of all L networks are fused in a fully connected network, all are trained together. The evaluation is with the ADNI-1 dataset as a training set and ADNI-2 as a test dataset. The model achieves 51.8% accuracy in a 4-class classification (11.4% above state-of-the-art benchmarks) and an improvement of 8.7% in regression RMSE on four clinical brain status scores (Clinical Dementia Rating Sum of Boxes, classic Alzheimer’s Disease Assessment Scale Cognitive (ADAS-Cog) subscale with 11 items, modified ADAS-Cog with 13 items, and Mini-Mental State Examination).

2.6 Other data analysis tasks for Deep Learning in brain imaging

Finally, we mention here three additional recent works about deep learning in brain imaging data analysis, presenting novel deep learning solution approaches which may be relevant for different medical problems.

[31] use a 3D CNN to produce a motion probability map for the analysis process of cortical MRI. Their network estimator manages to account for variations in cortical thickness that are due to subject motion during the scan, thus enabling a better discriminative analysis and grouping of MRI scan results. The method was tested both on the ABIDE dataset and on a dataset collected by the authors, and may be applicable to other MRI data as well.

[34] propose an encoder-decoder network with a spatial transformer module (see [32]) for multi-input MR image synthesis. They evaluate their network on the SISS dataset from the Ischemic Stroke Lesion Segmentation (ISLES) 2015 challenge, and in the multi-modal Brain Tumor Segmentation (BRATS) 2015 challenge dataset.

Another work, [23], suggests a deep learning method for separating relevant vs. non-relevant imaging signals. They focus on the analysis of MEG scans, where signal from muscle activity, and very commonly, eye blinks, corrupts the data. In the current practice, this problem is usually treated by affixing eye proximal electrodes and recording eye movement in addition to the MEG data. In this paper the authors suggest a data-based deep learning solution for the same problem. They show that a simple CNN can be trained for identifying eye-blink related signals. Their model achieves accuracy, recall and precision all above 97% on a dataset of 14 patients, in a leave-one-out cross-validation scheme.

Deep Learning in Brain Imaging – References

(*) Descoteaux, M., Maier-Hein, L., Franz, A., Jannin, P., Collins, D.L., Duchesne, S. (eds.) Medical Image Computing and Computer-Assisted Intervention MICCAI 2017. Springer International Publishing, Cham (2017)

[9] Bahrami, K., Rekik, I., Shi, F., Shen, D.: Joint reconstruction and segmentation of 7t-like mr images from 3t mri based on cascaded convolutional neural networks. Printed in (*) pp. 764–772.

[11] Baur, C., Albarqouni, S., Navab, N.: Semi-supervised deep learning for fully convolutional networks. Printed in (*) pp. 311–319.

[13] Bortsova, G., van Tulder, G., Dubost, F., Peng, T., Navab, N., van der Lugt, A., Bos, D., De Bruijne, M.: Segmentation of intracranial arterial calcification with deeply supervised residual dropout networks. Printed in (*). pp. 356–364.

[14] Chen, J., Banerjee, S., Grama, A., Scheirer, W.J., Chen, D.Z.: Neuron segmentation using deep complete bipartite networks. Printed in (*). pp. 21–29.

[19] Dosovitskiy, A., Fischer, P., Ilg, E., Hausser, P., Hazirbas, C., Golkov, V., van der Smagt, P., Cremers, D., Brox, T.: Flownet: Learning optical flow with convolutional networks. In: Proceedings of the IEEE International Conference on Computer Vision. pp. 2758–2766 (2015)

[20] Dubost, F., Bortsova, G., Adams, H., Ikram, A., Niessen, W.J., Vernooij, M., De Bruijne, M.: Gp-unet: Lesion detection from weak labels with a 3d regression network. Printed in (*). pp. 214–221.

[22] Fidon, L., Li, W., Garcia-Peraza-Herrera, L.C., Ekanayake, J., Kitchen, N., Ourselin, S., Vercauteren, T.: Scalable multimodal convolutional networks for brain tumour segmentation. Printed in (*). pp. 285–293.

[23] Garg, P., Davenport, E., Murugesan, G., Wagner, B., Whitlow, C., Maldjian, J., Montillo, A.: Using convolutional neural networks to automatically detect eye-blink artifacts in magnetoencephalography without resorting to electrooculography. Printed in (*). pp. 374–381.

[25] Ghafoorian, M., Mehrtash, A., Kapur, T., Karssemeijer, N., Marchiori, E., Pesteie, M., Guttmann, C.R.G., de Leeuw, F.E., Tempany, C.M., van Ginneken, B., Fedorov, A., Abolmaesumi, P., Platel, B., Wells, W.M.: Transfer learning for domain adaptation in mri: Application in brain lesion segmentation. Printed in (*). pp. 516–524.

[27] Gupta, V., Thomopoulos, S.I., Rashid, F.M., Thompson, P.M.: Fibernet: An ensemble deep learning framework for clustering white matter fibers. Printed in (*). pp. 548–555.

[29] Hou, B., Alansary, A., McDonagh, S., Davidson, A., Rutherford, M., Hajnal, J.V., Rueckert, D., Glocker, B., Kainz, B.: Predicting slice-to-volume transformation in presence of arbitrary subject motion. Printed in (*). pp. 296–304.

[31] Iglesias, J.E., Lerma-Usabiaga, G., Garcia-Peraza-Herrera, L.C., Martinez, S., Paz-Alonso, P.M.: Retrospective head motion estimation in structural brain mri with 3d cnns. Printed in (*). pp. 314–322.

[32] Jaderberg, M., Simonyan, K., Zisserman, A., kavukcuoglu, k.: Spatial transformer networks. In: Cortes, C., Lawrence, N.D., Lee, D.D., Sugiyama, M., Garnett, R. (eds.) Advances in Neural Information Processing Systems 28, pp. 2017–2025. Curran Associates, Inc. (2015)

[33] Johansen-Berg, H., Behrens, T.E.: Diffusion MRI: from quantitative measurement to in vivo neuroanatomy. Academic Press (2013)

[34] Joyce, T., Chartsias, A., Tsaftaris, S.A.: Robust multi-modal mr image synthesis. Printed in (*). pp. 347–355.

[37] Kingma, D.P., Salimans, T., Welling, M.: Variational dropout and the local reparameterization trick. In: Cortes, C., Lawrence, N.D., Lee, D.D., Sugiyama, M., Garnett, R. (eds.) Advances in Neural Information Processing Systems 28, pp. 2575–2583. Curran Associates, Inc. (2015), http://papers.nips.cc/paper/5666-variational-dropout-and-the-local-reparameterization-trick.pdf

[39] Ktena, S.I., Parisot, S., Ferrante, E., Rajchl, M., Lee, M., Glocker, B., Rueckert, D.: Distance metric learning using graph convolutional networks: Application to functional brain networks. Printed in (*) pp. 469–477.

[41] Lafferty, J., McCallum, A., Pereira, F.C.: Conditional random fields: Probabilistic models for segmenting and labeling sequence data (2001)

[44] Liu, M., Zhang, J., Adeli, E., Shen, D.: Deep multi-task multi-channel learning for joint classification and regression of brain status. Printed in (*). pp. 3–11.

[50] Poulin, P., Côté, M.A., Houde, J.C., Petit, L., Neher, P.F., Maier-Hein, K.H., Larochelle, H., Descoteaux, M.: Learn to track: Deep learning for tractography. Printed in (*) pp. 540–547.

[53] Ronneberger, O., Fischer, P., Brox, T.: U-net: Convolutional networks for biomedical image segmentation. In: Navab, N., Hornegger, J., Wells, W.M., Frangi, A.F. (eds.) Medical Image Computing and Computer-Assisted Intervention – MICCAI 2015. pp. 234–241. Springer International Publishing, Cham (2015)

[57] Shen, H., Wang, R., Zhang, J., McKenna, S.J.: Boundaryaware fully convolutional network for brain tumor segmentation. Printed in (*). pp. 433–441.

[60] Tanno, R., Ghosh, A., Grussu, F., Kaden, E., Criminisi, A., Alexander, D.C.: Bayesian image quality transfer. In: International Conference on Medical Image Computing and Computer-Assisted Intervention. pp. 265–273. Springer (2016)

[61] Tanno, R., Worrall, D.E., Ghosh, A., Kaden, E., Sotiropoulos, S.N., Criminisi, A., Alexander, D.C.: Bayesian image quality transfer with cnns: Exploring uncertainty in dmri super-resolution. Printed in (*) pp. 611–619.

[62] Uzunova, H., Wilms, M., Handels, H., Ehrhardt, J.: Training cnns for image registration from few samples with modelbased data augmentation. Printed in (*) pp. 223–231.

[70] Ye, C.: Learning-based ensemble average propagator estimation. Printed in (*) pp. 593–601.

[71] Ye, C., Prince, J.L.: Fiber orientation estimation guided by a deep network pp. 575–583 (2017)