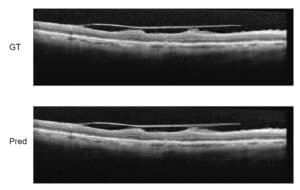
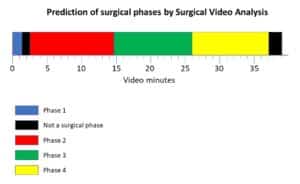
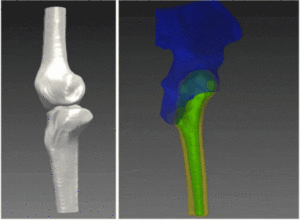
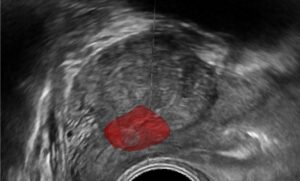
In search for a pattern in an image, a video or a signal, one has to consider several sources of bias, noise and uncertainties. Such uncertainties are the result of acquisition of natural signals such as outdoors images in non-sterile and poorly lit conditions, possibly containing smear, blurs, artifacts and partial occlusion of the pattern searched for. Such problems naturally promote the use of statistical methods in pattern recognition methodologies. By pattern we mean any symbol or geometrical form which can be stripped from details and searched for in the image. Expanding the notion of a pattern to the spatiotemporal domain, a dynamical pattern can be searched for, such as signature of motion. Whether on temporal, spatial or frequency domains, the template pattern must first be defined and its salient feature extracted.

The statistical nature of pattern recognition and classification can be seen even in applications where a template is searched exhaustively in an input image, a measure of similarity between the template and the image is devised and a threshold is used to make a decision regarding the match. The similarity measure is used like in a hypothesis test, in which the null hypothesis (stating that the observed image sub-region does not contain a pattern) is ruled by the threshold value. A more sophisticated interpretation is given in the Bayesian framework, where the value of conditional probability that the image sub-region contains the pattern given a template, becomes the similarity measure and the decision is made in favor of the conditional probability with the highest obtained value.
A relatively recent and natural language for formalizing the inherent uncertainty in both the feature extracted and the data is that of the fuzzy sets. Fuzzy sets is a framework in which a sample set has a predefined (crisp) membership function obtaining values between 0 and 1. A generalization of the fuzzy set is the fuzzy set of type 2 (interval fuzzy sets) in which each value of the membership function is itself a fuzzy set (an interval between 0 and 1). This means that the crisp (deterministic) membership function has a lower and upper bound for each membership value. With this approach, the score obtained for a pattern found in an image can fall within the interval of uncertainty provided by the type 2 fuzzy set membership function. Type 2 interval fuzzy sets partially relieves us from the burden of correcting for time varying noise, for example. The membership function itself can be constructed, with its boundaries of uncertainties, using training data for each pattern class.
There are many techniques to search for and score pattern in the image based on a template. In the search process, a candidate sub region of the image the patterns might appear in should first be identified. Learning the salient features of a template and searching for them allows us to avoid the exhaustive search within the image for a certain signature by only working in the feature space. Further reduction of search time can be achieved by searching on an image grid or a low resolution version of the original image. Pyramid of resolution can also be employed to search in several scales and reduce the risk of false positive sub-regions containing the pattern.
However, these all depend on the nature of the input data and patterns to be searched for. Regardless of the method employed to find a candidate pattern and a score, a decision must be made regarding its membership to one class or another. In terms of fuzzy control system, this process is called defuzzification. This is basically an interpretation of the membership values into fuzzy decision or class membership probability.
Integration of type two fuzzy set decision making in pattern classification allows the incorporation of uncertainties, bias and noise. These are all part of real world problems, which type 2 interval fuzzy sets provide mathematically sound language to work with. In many ways, the decision based on uncertainties are included among the techniques of machine learning; only that the decision made regarding membership is taken based on deterministic laws (e.g. a sample falling to the right or left of a decision line), whereas fuzzy control permits more flexible and natural soft decisions, which mimic in many ways the judgment made by humans.
RSIP Vision stands in the forefront of technological development in the domain of image processing and computer vision machine learning. As such, RSIP Vision incorporates new methodologies to improve the performance of our algorithms in real life applications.
A relatively recent and natural language for formalizing the inherent uncertainty in both the feature extracted and the data is that of the fuzzy sets. Fuzzy sets is a framework in which a sample set has a predefined (crisp) membership function obtaining values between 0 and 1. A generalization of the fuzzy set is the fuzzy set of type 2 (interval fuzzy sets) in which each value of the membership function is itself a fuzzy set (an interval between 0 and 1). This means that the crisp (deterministic) membership function has a lower and upper bound for each membership value. With this approach, the score obtained for a pattern found in an image can fall within the interval of uncertainty provided by the type 2 fuzzy set membership function. Type 2 interval fuzzy sets partially relieves us from the burden of correcting for time varying noise, for example. The membership function itself can be constructed, with its boundaries of uncertainties, using training data for each pattern class.
There are many techniques to search for and score pattern in the image based on a template. In the search process, a candidate sub region of the image the patterns might appear in should first be identified. Learning the salient features of a template and searching for them allows us to avoid the exhaustive search within the image for a certain signature by only working in the feature space. Further reduction of search time can be achieved by searching on an image grid or a low resolution version of the original image. Pyramid of resolution can also be employed to search in several scales and reduce the risk of false positive sub-regions containing the pattern.
However, these all depend on the nature of the input data and patterns to be searched for. Regardless of the method employed to find a candidate pattern and a score, a decision must be made regarding its membership to one class or another. In terms of fuzzy control system, this process is called defuzzification. This is basically an interpretation of the membership values into fuzzy decision or class membership probability.
Integration of type two fuzzy set decision making in pattern classification allows the incorporation of uncertainties, bias and noise. These are all part of real world problems, which type 2 interval fuzzy sets provide mathematically sound language to work with. In many ways, the decision based on uncertainties are included among the techniques of machine learning; only that the decision made regarding membership is taken based on deterministic laws (e.g. a sample falling to the right or left of a decision line), whereas fuzzy control permits more flexible and natural soft decisions, which mimic in many ways the judgment made by humans.
RSIP Vision stands in the forefront of technological development in the domain of image processing and computer vision machine learning. As such, RSIP Vision incorporates new methodologies to improve the performance of our algorithms in real life applications.