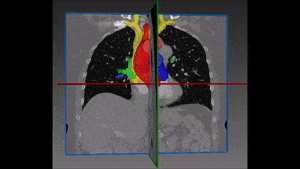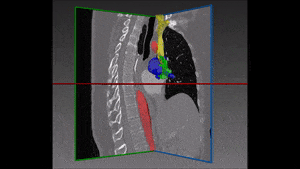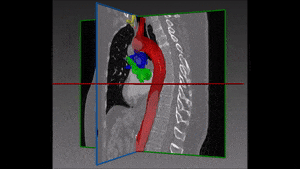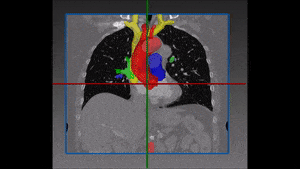
Converting these differences into code is indeed quite challenging: if images are not physiologically consistent -for instance if they do not capture entirely the same region – it is difficult to align them and build a powerful statistical shape model. On the other hand, the task of building a left ventricle shape model can also prove itself very valuable: suffice it to say that cardiovascular diseases are the largest cause of death in the developed world, responsible for two million deaths per year only in Europe.
After a myocardial infarction, the heart alters itself to preserve physiological constraints: the question is whether and how a probabilistic model of the left ventricle, the cardiac chamber in charge of pumping oxygenated blood to distant tissue in the entire body, is able to detect myocardial infarction and correctly predict a patient’s heart disease status. A robust and properly validated detection model of myocardial infarction built on a left ventricle shape model would be extremely precious with regard to both scientific research and clinical treatment.
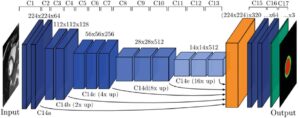
Of the several methods which could be used to generate a left ventricle shape model, we find that the most promising one is based on a partial least squares technique which searches for new axes of variation that correlate best with an output variable such as the clinical diagnostic (the disease states), through a decomposition method that is anatomically and clinically more meaningful. Partial least squares is a calibration method often used as a regression tool for prediction of anatomical and clinical data in medical imaging.
Using a single diagnostic variable Y to label healthy and infarcted hearts (0 for healthy subjects and 1 for infarcted hearts), we can run a regression so that for each new subject the unknown diagnostic variable (healthy or infarcted heart) could be predicted with the highest possible accuracy, based on the subject-specific shape (being the input variable X). The role of partial least squares is to perform a simultaneous decomposition of X and Y such that the score vectors which are obtained along the new representation axes of both the input and output matrices correlate best, regardless of what is the triggering factor behind this correlation. This leads to maximal interdependency between the two variables (the given shapes and the health state of the heart) as well as highly accurate predictions of the output (in the order of 98%). The decomposition is obtained through NIPALS (non-linear iterative partial least squares), an algorithm employed to compute the first few components in partial least squares or principal component analysis.
With this decomposition, the new shape components are those that maximize correlation with the clinical status (the output), leading to models that are scientifically and clinically more meaningful. These new components can now be used with the regression model introduced above to discriminate between healthy and infarcted hearts, in order to enable this left ventricle shape modelling technique to predict the cardiac state of the patient.

 Cardiology
Cardiology